2015년 4월 2일 목요일

mmd ch10 Mining Social-Network Graphs

10 Mining Social-Network Graphs

페이스북 친구 관계처럼 그래프로 그려 낼수 있는 데이터는 많다. 우리는 해당 소셜 네트워크에서 커뮤니티를 찾아 내는 방법을 공부할것이다. 해당 알고리즘은 클러스터링과 비슷하게 보일수도 있지만 커뮤니티가 중첩될수 있다는 부분이 다르다. 예를 들어 페이스북 친구들에서 커뮤니티를 찾아낸다면 A는 대학교 커뮤니티면서 A는 고등학교 커뮤니티에 동시에 속할수 있다. 해당 부분에 대해서 공부해보자
  1. 10.1 Social Networks as Graphs
    소셜 네트워크 그래프 모델에 대해서 공부해 보자 소셜 네트워크 특징은 안의 노드들이 동일한 커뮤니티에 속해 있을 경우 클러스터링 되어 있다는것이다.
  2. 10.1.1 What is a Socail Network?
    우리는 페이스북, 트위터 ,구글+ 등을 보고 소셜 네트워크라고 부른다. 즉 사회적인 관계를 표현한 네트워크 란 의미이다. 자 소셜 네트워크 주된 특징은 무엇일까?
    • 네트워크에 참여하는 entities 들이 있으며 대체적으로 사람이다(하지만 다른경우도 있음)
    • entities 사이에 관계가 존재한다. 관계의 종류는 다양하며 페이스북에서는 친구 이며 관계는 친구이거나 아니거나로 표현된다. 하지만 구글+에서는 관계가 숫자로 나타난다. 친구, 가족 등 (예를 들면 두사람이 대화하는 날짜/모든 사람이 평균적으로 대화하는 날짜 같은 비율로 나타난다.)
    • nonrandomness 또는 locality 라는 가정이 존재한다. 관계가 있는 애들은 클러스터링 되어 있을 가능성이 높다라는 가정이다. 예를 들어 A가 B 와 C 에게 연결 관계가 있으면 B 와 C 가 서로 알 가능성이 평균에 비해 훨씬 높다는것이다.
  3. 10.1.2 Social Networks as Graphs
    소셜 네트워크는 그래프를 이용해서 모델링 할수있다. 소셜 그래프라고 불린다.
    엔터티는 노드라고 부르며 에지는 두 노드간의 관계를 표현한다. 만약 엣지에 등급(degree)을 줘야 하면 엣지에 레이블을 붙여서 표현 할수 있다. 소셜 그래프는 방향성이 있을 수도 (twiter followe) 없을 수도 있다. (facebook friend)
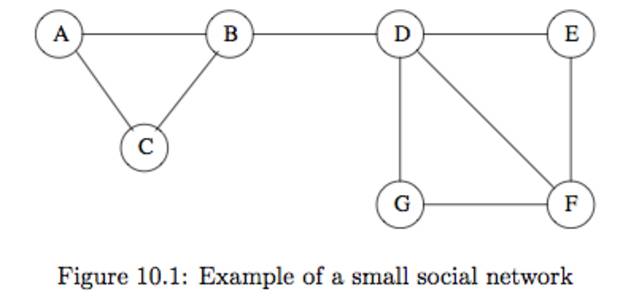
    alt text
     ex(10.1)
  figure 10.1 은 A~G까지는 사람이고 각 엣지는 친구 관계를 나타낸다. 예를 들면 B는 A,C,D와 친구이다.
    위의 그래프에서 locality 를 확인해 보자 9개의 엣지와 7개의 노드가 있다.
    노드간 존재 할수 있는 엣지의 총수는 {7\choose 2} = 21 이다.
    위의 그래프에서 X,Y,Z 를 뽑는다고 생각해보자(예를 들어 X = A, Y = B, Z = C)
    X,Y가 연결되어있고 X,Z가 연결되어 있을떄 Y,Z 가 연결될 확률을 구해보자
    물런 그래프가 엄청크다면 확률을 9/21 = 0.429 일것이다. 하지만 그래프가 작음으로 진짜 확률과 비율의 차이를 볼수 있다. 이미 (X,Y),(X,Z)의 연결이 존재함으로 엣지는 7개 노드는 19 개가 남아있다 즉 (Y,Z)의 확률은 7/19 = 0.368 이라는걸 알수있다.
    하지만 정말로 위의 그래프에 X,Y,Z를 대입해서 구해보자 X가 정해질 경우 Y,Z의 순서는 상관없다.
    X 가 A 라면 B,C 의 노드만 가능하고 두개가 연결되어 있음으로 +1 이라고 하자
    위의 상황은 X가 C,E,G 일때도 동일하다.
    X 가 F 라고 하면 F는 3개의 이웃노드를가지고 있고 (D,E,G) Y, Z가 D,E 또는 D,G일 경우 엣지가 존재한다. 하지만 E,G일 경우 엣지가 존재하지 않는다. +2, -1 이라고 하자
    X 가 B라면 +1 = {(A,C)}, -2 = {(A,D).(C,D)} 가된다.
    X 가 D라면 +2 = {(E,F),(G,F)}, -4 = {(B,G),(B,E),(B,F),(E,G)}가된다.
    위의 모든 수를 계산하면 +9, -7의 경우를 알수있다. 그렇다면 실제 가지고 있을 확률은 9/16 = 0.563이다. 이 확률은 0.368 에 비해 충분이 크다 그러므로 관계가 있는 애들끼리는 다른 애들보다 관계가 있을 확률이 높다는 locality 를 증명한다.
  1. 10.1.3 Varieties of Social Networks
    locality 와 relationships 속성이 있는 다른 종류의 소셜 네트워크를 나열해보자
    • Telephone Networks
      노드는 전화번호이며 특정한 기간에 A 와 B가 전화로 연결되었으면 관계가 있다고 정의하고 그 해당 기간 동안에 연결된 횟수를 degree로 나타낼수 있다.
    • Email Networks
      노드는 이메일이며 두개의 주소가 한번이라도 이멜을 발송(or 수신)한적이 있으면 관계가 있다고 보자(스팸머를 피할려면 수신,발신 둘다 있을때로 정의)또는 한쪽간의 연결관계가 있으면 약함 양쪽도 있으면 강함으로 나타낼수도 있다.
    • Collaboration Networks
      노드는 개인이며 연결과계는 같은 논문을 공동 저자로 나올때 생긴다고 보자 또는 논문을 노드로 보고 두 논문에 같은 저자가 있으면 연결관계를 만든다로 정의 할수도 있다.
      또한 양방향 관계가 있는 경우는 관계를 나타낼수 있다. 예를 들어 위키 피디아의 editior을 노드로 보고 두 editer가 동일한 article을 수정했다면 관계를 맺을수있다.
      ch9에 나오는 유저와 공산물과의 관계도 네트워크로 나타낼수도 있다. 예를 들어 동일한 물건을 산 유저들을 하나의 커뮤니티로 볼 수 있다.
      반대로 동일한 유저들에 의해 구매된 공산물들을 하나의 커뮤니티로 볼수있다.
    • other Examples of Social Graphs
      다른 종류의 많은 현상들도 소셜 그래프로 볼수있다 특히 locality 를 가지고 있다면..
      inforamtion networks(documents, web garph, patents)
      biological networks(genes, proteins, food-web of animal each other)
      product co-puchaing networks
  1. 10.1.4 Graphs With Serveral Node Types
    여러종류의 노드 타입을 같는 현상들이 존재한다.
    우리가 조금전에 이야기한 collaboration networks 의 경우 user 와 proudct의 2가지 노드로 구성되어 있다.
    또한 조금전에 이야기한 논문의 경우 논문, 저자로 표현할수있다.(좀전에는 둘중 하나를 없애서 표현한 경우 이다.)
    좀더 복잡한 예를 들자면 유저가 페이지에 주제별로 테깅을 한다고 생각해보자 3개의 종류의 노드가 존재하는경우이다.
    이럴 경우 k-partite 그래프라고 하며 k > 1 보다 크다. k-partite 그래프는 k 의 서로 다른 set 으로 구성되며 같은 set 끼리는 엣지가 없다.
     ex10.2)
 users = {U1,U2}
 tags = {T1,T2,T3,T4}
 webPages = {W1,W2,W3} 가 존재한다고 하고 
 {U1,T2}의경우 user1이 T2를 태깅했다고 생각하자 
 {T2,W2}의 경우 w2 page에 T2태그가 태깅된 것이다.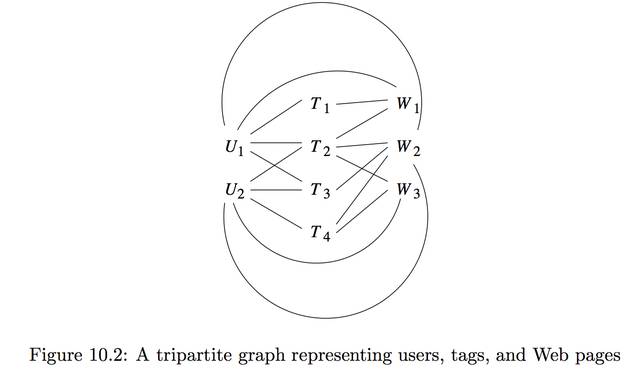
    alt text
  1. 10.2 Clustering of Social-Network Graphs
    소셜 네트워크의 경우 하나의 노드가 여러커뮤니티에 속할 수 있음으로 ch7 에서 이야기한 알고리즘이 잘맞지 않는다.
    (A노드는 고등학교 커뮤니티에 속하면서 대학교 커뮤니티에도 속할수 있다.)
  1. 10.2.1 Distance Measures for Social-Networks Graphs
    일단 클러스터링을 할려면 거리를 측정하는 방법을 정해야 한다 만약 그래프 사이에 degree가 존재하면 해당 정도를 쓸수 있지만 그렇지 않은 그래프가 더 많다 예를 들어 페이스북의 경우 친구이거나 아니거나 이다. 예를 들어 우리가 친구 이면 0 아니면 1이라고 거리를 정한다고 생각해보자 (거리기 때문에 가까울수록 작다) 또는 친구이면 1 아니면 무한대 라고 할 경우 해당 측정은 삼각 거리 ( triangle inequality)측정에 위배 된다. 예를 들면 (A,B)그리고 (B,C)가 친구이고 (A,C)가 친구가 아니라면 A -> C = 1 이고 A -> B -> C 는 0 이된다 삼각거리가 성립될려면 거처서 연결된 점은 바로 연결된 점보다 같거나 커야 된다.
  1. 10.2.2 Applying Standard Clustering Methods
    만약 우리가 일반적인 클러스터링 알고리즘 중 hierarchical 을 사용한다고 가정하면 우리는 거리를 측정 할수 없게 연결된 두 노드중 랜덤으로 뽑아서 결합 할것이다. 그래프가 크가면 결과 또한 랜덤하게 나옴으로 클러스터링 된다고 할 수 없다.
     위의 그림에는 {A,B,C}와 {D,E,G,F}클러스터가 존재한다고 볼수 있다 문제는 어떻게 해당 클러스터를 찾아낼수 있을까이다.
    다음으로는 kmean을 사용한다고 가정해보자 k=2 이고 우리가 정말 잘뽑아서 시작점을 B,와 F를 뽑앗다고 하자 D는 어디에 속해야 하는가? 정확이 F에 속한다고 인간은 판단하지만 알고리즘에서는 랜덤하게 됨으로 해당 알고리즘도 사용할수 없다.(D를 제일 마지막에 배치한다고 하고 주변에들과 비교해 가장 가까운 쪽
    에 붙일수 있지만 그래프가 커지면 에러가 생길수 있는 로직이다.)
  1. 10.2.3 Betweenness
    위에서 설명한 문제들을 해결하기 위해 여러 클러스터링 방법론이 만들어졌고 그중 심플한 알고리즘을 소개한다.
    기본 아이디어는 커뮤니티에 속하지 않을 가장 그럴사한 엣지를 찾아내는것이다.
    betweeness 라는걸 엣지 (a,b)사이에 존재하는 모든 노드 쌍x,y의 가장 짧은 거리(shortest path)라고 정의하자
    betweeness가 클수록 해당 엣지를 커뮤니티를 분리하는 엣지로 정의하는 방법이다.(아래에 상세 설명됨)
    참고:Betweenness centrality
  2. 10.2.4 The Girvan-Newman Algorithms
    엣지들의 betweenness 를 계산하기 위해서 우리는 각 엣지들을 지나는 shortest paths 들의 숫자를 새야한다.이방법중 하나인 Girvan-Newman(GN)알고리즘을 소개한다. 우리는 그래프의 모든 노드를 돌면서 해당 노드에서 다른 노드까지의 shortest path를 구할것이다. 해당 알고리즘은 그래프에 BFS(breath-first serach)를 행함으로 시작된다. BFS 표현에서 레벨은 X에서 해당 노드까지 갈수 있는 shortest path의 길이를 의미한다. 그러므로 같은 레벨에 있는 노드들끼리의 엣지는 X를 기준으로 절대 shortest path가 될수 없다.
    레벨사이에 존재하는 엣지들을 DAG 엣지라고 부르자(directed acyclic graph). 모든 DAG 엣지들은 루트 X에서부터 다른 노드들 사이를 가장 잛게 연결하는 shortest path의 일부분이 된다.
    만약 (Y,Z)의 DAG엣지가 존재한다고 가정하자 이떄 Y노드의 레벨이 Z노드보다 루트에 가까운 레벨의 노드라면 Y를 Z의 parent, Z를 Y의 자식 이라고 호칭하자 (부모가 유니크할 필요는 없다.)
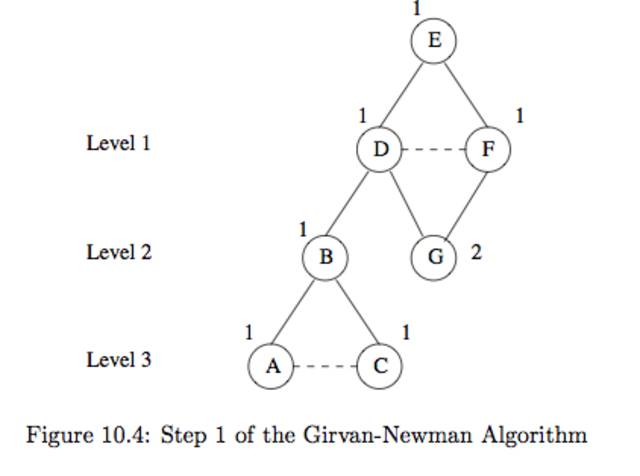
    alt text
     ex10.6)f10.4를 보면 f10.3을 BFS로 표현한것이다. 루트는 E이다.
 1. 그래프를 BFS로 표현한다.
 2. 루트에 1을 표시하고 트리를 내려가면서 모든 자식 노드들의 점수는 연결된 부모노드의 점수의 합계로 정의한다.

     ex10.7)위의 2번째 스탭을 자세이 설명해 보자 
 1. E는 루트임으로  E는 1
 2. D,F의 부모는 E임으로 각각D,F는 1
 3. B의 부모는 D임으로 D는 1, G의 부모는 D,F임으로 합계 G는 2
 4. A,C의 부모는 B임으로 각각 A,C는 1
    3번쩨 스탭은 각각의 엣지 e의점수를 계산한다.
    e의 점수 = 루트 X에서 엣지e 를 통해 Y로 가는 모든 shortest path / 루트 X에서 Y로 가는 모든 shortest path
    해당 점수를 계산하는 방법은 아래와 같다.
     1. 모든 DAG 엣지의 leaf노드는 1점을 부여한다.
 2. 리프노드가 아닌 모든 노드들은 해당 노드에 DAG엣지의 합계 + 1을 부여한다.
 3. Z으로 들어오는 엣지e의 점수는 루트에서 Z으로 e를 통해 들어오는 모든 shortest path / Z로 들어오는 모든 shortestpath 이다.
    3.1 위의 식을 좀 추상화 하면 Z의 부모를 Y_{1},Y_{2},\dots,Y_{K}라고 할때 p_{i}를 루트로 부터 Y_{i}로 들어오는 shortest path의 수량이라고 하자(fig10.4의 점수)그러면 우리는 엣지(Y_{i},Z)의 점수를 \frac{Z * p_{i}}{\sum_{j=1}^kp_{j}}라고 할수 있다 위식의 Z는 위의 2번 규칙에 때라 각 노드에 부여한 점수이다.
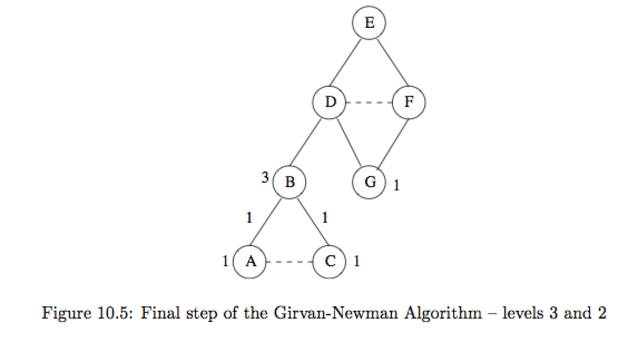
    alt text
     ex10.8)위의 f10_5를 보자 우리는 맨아래 3레벨에서 부터 계산해 올라갈것이다. 
 1. 3레벨의 A와 C는 리프임으로 1을 같는다.
 2. 각 노드들은 하나의 부모를 같고 있음으로 엣지(B,A),(B,C)에 각각 1점을 부여한다.
 3. 2레벨의 G는 리프임으로 1, B는 리프가 아님으로 자기에게 들어오는 엣지의 합 + 1를 주면 3이된다.
 (B가 3인이유는 B를 통과해 가는 shortest path 가 많기 때문이다.)
 4. 1레벨로 가면 B는 D하나만 부모로 가짐으로 (B,D)는 3이다. G의 경우 (D,G),(F,G)를 가짐으로 점수를 분리한다
 근대 무슨 기준으로 분리해야할까? fig10.3의 D,F가 각각 1점임을 알수 있고(Root E에서 각각,D,F로 갈수 있는 shortest path의 수) 위의 3.1의 식을 적용하면 1*1/1+1 즉 각각 0.5 임을 알수 있다.
 5. 1레벨노드를 계산하면 D는 엣지합(3.5) + 1 = 4.5, Fsms 0.5 + = 1.5임을 알수있다.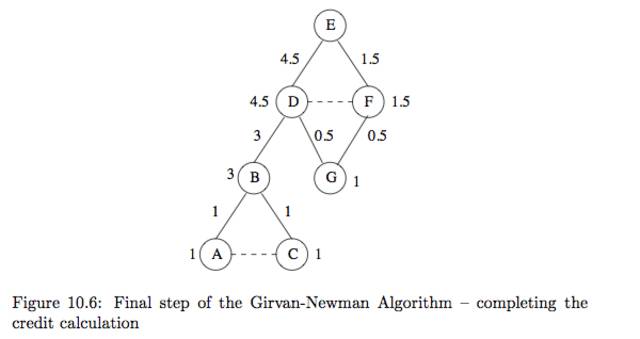
    alt text
    우리가 모든 노드에 대하여 위의 알고리즘을 돌리면 모든 관계가 2번씩 발견됨으로 2로 나누어 주어야된다.
  3. 10.2.5 Using Betweenness to Find Communities
    betweeness 점수는 그래프에서 각 노드들간의 distance measure 와 비슷하다.(물런 정확히 그렇지는 않다 왜냐하면 연결되지 않은 노드끼리의 점수는 정의 되지 않았기 때문에 또한 정의한다고 해도 triangle inequality를 만족하지 못할것이다.)
    어째든 우리는 betweenness를 증가 하는 순서대로 하나씩 붙임으로써(작은 점수부터) 조금씩 큰 클러스터를 만들수 있다.
    위의 아이디어는 edge removal로 표현될수 있다 그래프를 모든 연결된 엣지에서 시작해 높은 betweeness 엣지를 삭제해 나간다 (만족할 만한 커뮤니티 그룹을 찾을때까지)
     ex10.9)f10_7을 보면 우리가 구한 betweeneess점수가 모든 엣지에 적혀있다.(아래 점수는 reader기분으로 왼쪽에서 부터 계산된 결과이다 )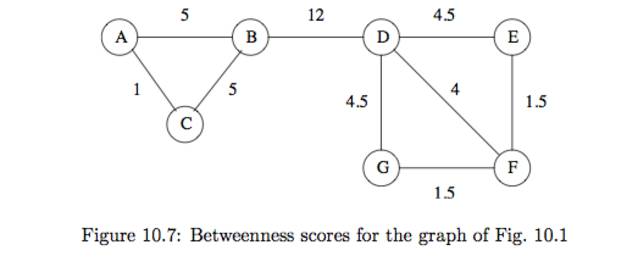
    alt text
     일단 (B,D)가 가장높은 점수임으로 삭제한다 그러면 {A,B,C}와 {D,E,F,G}로 클러스터링 할수있다. 하지만 우리가 계속 높은 점수대로 제거해 나가면 {A,C},{B},{D},{E,F,G}로 나누어진다.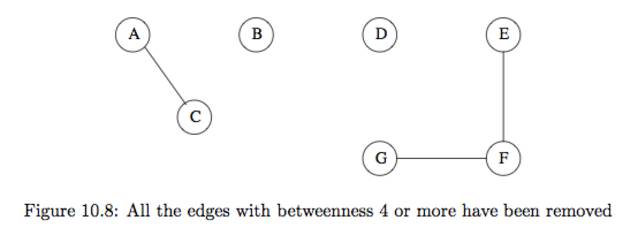
    alt text
    위의 그림은 조금 이상하게 느껴진다. 하지만 {A,C}가 연결되고 B가 분리된 이유는 B가 외부와 연결하는 통로이기 떄문이다.{E,G,F} 와 D도 동일한 맥락에서 이해 할수 있다.

정리중..


원본책  http://www.mmds.org
​
작성자:
라벨: ,