유사한 두개 회사의 동일 데이터를 찾아서 통합해라
1. 목적
- 기본문제: 두개 회사에 유저셋1, 유저셋2가 있다 해당 유저중 비슷한 유저를 찾아서 통합해라
- 필자문제: 두개 회사에 장소셋1, 장소셋2가 있다 해당 장소중 비슷한 장소를 찾아서 통합해라
- 그림 설명아래 그림을 보면 투어라는 회사에서 어떤 장소를 선택한 후 유사도 검색을 하면 위시빈 이라는 회사의 장소에서 가장 유사한 애들을 나열 한후 유사도를 보고 아래 통합 버튼을 눌러서 통합 할 수 있다.
- 유사도 0.5 이상이 존재하는경우 1
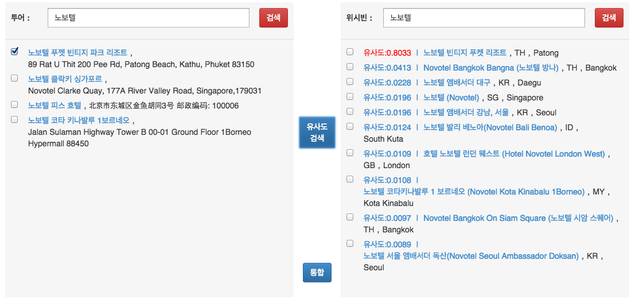
- 유사도 0.5 이상이 존재하는경우 2
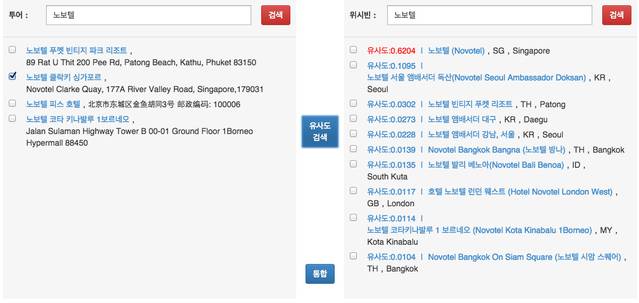
- 존재하지 않는 경우
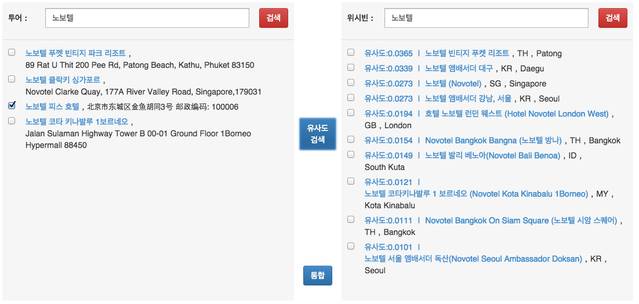
- 목적 설명필자의 경우 투어 회사의 데이터가 적었기 때문에 완전 자동화 할필요는 없었다.(구현 시간보다 사람이 하는게 더빠르다….) 그래서 기본적인 툴만 만들어 주면 되었다 만약 비교할 데이터가 많았으면 LSH 알고리즘을 사용해서 유사항 쌍을 찾고 특정 한계값을 기준으로 통합 시키고 남은 애들만 사람이 수동으로 통합하거나 버리거나 하는 방법을 사용했을거 같다.
- 데이터가 조금이라도 많아지면 시간 복잡도는 O(M*N)에 유사도를 계산하는 비용까지들어가야한다… LSH를 사용하지 않고 하나의 장소를 다른 셋의 모든 데이터와 비교하는건 힘들다.
- 유사도 계산문제는 어떻게 해당 애들의 유사도를 계산하느냐이다 일단 유사할것이라고 예측하는 4개의 필드를 뽑았다. 필자의 경우 최초 장소명으로 검색을 했지만 필요하다면 LSH를 사용해서 전체를 대상으로 비교 할수도 있다.또는 장소일 경우는 특정 범위를 기준으로도 가능하다
- 장소명
- 장소 전화번호
- 장소 홈페이지
- 장소 위도,경도
위의 필드를 사용해서 어떻게 유사도를 계산을 할까?
각속성별 계산방법
- 장소명 속성장소명의 경우 아래와 같이 동일한 스팟의 경우에도 이름이 다를 수있다. 최초 유사도로 edit distance 를 생각했지만
관련논문을 보고 2gram 후 jaccard similarity 를 사용했다.- 노보텔 클락키 싱가포르 | 노보텔 (Novotel)
function nGram(str){ return n_Gram(2)(str.replace(/\s/g,'').toLowerCase()); } nameSim = jaccard.index(nGram(wName),nGram(tName))jaccard.index(nGram('IFC 몰'),nGram('IFC 몰 (IFC Mall)')); //0.3
- 노보텔 클락키 싱가포르 | 노보텔 (Novotel)
- 장소 전화번호 속성전화 번호의 경우 동일하다면 해당 스팟이 동일한 스팟이라고 확신 할수 있을 정도다 (물론 앞부분에 국가 번호 (도시번호) 등의 특수 번호를 처리한다면…) 필자의 경우 특수 번호를 전처리 하지 않았기 떄문에 가중치를 주지는 않았다. 또한 전화번호의 경우 0~10까지의 숫자임으로 ngram후 jarccard를 할 경우 유사도를 잘 판단할수 없다.그래서 숫자추출 후 공백 문자로 분리 그 후 자카르 유사도를 계산했다.
function getNumberArr(str){ var temp = str.split(/\s/); for(var i = 0; i < temp.length;i++){ temp[i] = temp[i].replace( /^(\D+)/g, ''); } return temp; }jaccard.index(getNumberArr('+852 2295 3308'),getNumberArr('852 2295 3308')) //1 - 장소 홈페이지 속성해당 장소가 동일한 홈페이지(도메인) 주소를 가지고 있을 경우 동일한 스팟으로 볼수있다. 도메인만 추출 후 -> ngram 으로 후 자카드를 계산했다.
jaccard.index(nGram(parseUri('naver.com/aaaa/a')),nGram(parseUri('http://www.naver.com'))) //0.9 - 장소 위치 속성가장 중요한 부분이다. 해당 장소가 1000미터 이상 떨어질 경우(공원, 쇼핑몰 등은 폴리곤으로 만들지 않는이상 lat,lng가 차이날 가능성이 많다.) 0 1000 미터 이내일 경우 가까울수록 높은 유사도를 리턴 하도록 했다. 또한 가장 중요한 속성이라 고 생각했기 때문에 가중치 3배를 주었다.
distanceWeight = 3 function getDistanceProbability(a){ var max = 1000; var distance = Math.abs(max - a); return (distance >= max ? 1 : distance)/max; } distanceSim = getDistanceProbabilty(geolib.getDistance( {latitude: wLat, longitude: wLng}, {latitude: tLat, longitude: tLng} )); totPro += distanceSim * distanceWeight; totCnt += 1 * distanceWeight ;
결론
- 전체 유사도계산검색엔진에서 처리하듯이 그냥 유사도 점수로 계산했다
유사도 = 전체 sum / 카운트 - 결론threshold 를 0.5 로 잡은 결과 필자의 확인 결과로는 95%로 이상의 정확도를 보여줬다.
시간이 없어서 이쯤에서 마무리 하기는 했지만 재미 있었다.